fp64_sin(float64_NUMBER_PI) is not 0

Some people will be confused, when they are trying out the trigonometric functions of fp64lib the first time, e.g. with the following little Arduino program:

#include <fp64lib.h>

void setup() {
  Serial.begin(56000);
  float64_t x = fp64_sin(float64_NUMBER_PI );
  char *s = fp64_to_decimalExp( x, 17, false, NULL );
  Serial.print( "sin(pi) = " ); Serial.println( s );
}
void loop() {
}

fp64_sin( float64_NUMBER_PI ) returns not 0, but a very small positive number in the range of 1*10^-16! So, the library seems to have a bug.

No, it doesn’t. Not returning 0 is absolutely correct. But why?

This is due to the fact of π being an transcendential number, i.e. it has infinitely many digits, without repeating sequences. But in a computer, memory is not infinitely large. So, for doing numeric computations in a computer, π may only be approximated by a limited number of digits. Based on the number of available bits in a 64-bit-float, float64_NUMBER_PI is the best possible approximation of π.

But float64_NUMBER_PI is slightly smaller than π. As you may remember from school, sine starts at x=0 with a value of 0, has a peak value of 1 at x=π/2, then slowly decreases and touches 0 at x=π.

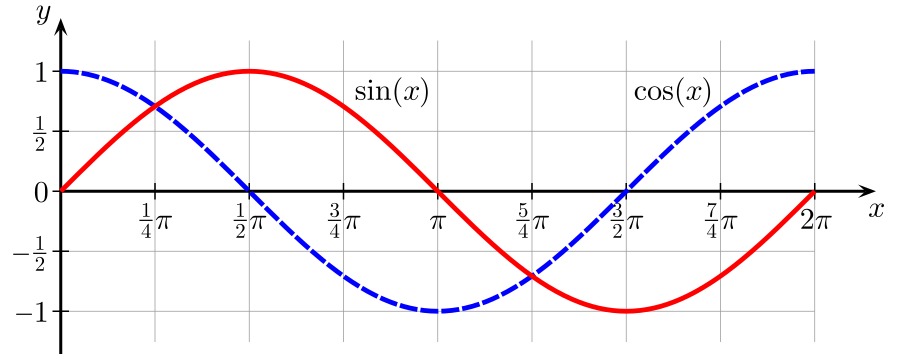
Source: Wikipedia, https://en.wikipedia.org/wiki/File:Sine_cosine_one_period.svg

For values x > π, the sin becomes < 0, has a minimum value of -1 at x = 3/2*π, slowly increases and touches 0 at x = 2*π. So the sine of a value slightly smaller than π returns a value slightly bigger than 0, and that’s why fp64_sin( float64_NUMBER_PI ) returns a very small positive number .

As a side note: If float64_NUMBER_PI is increased by 1 on the the least significand bit, then float64_NUMBER_PI would be already slightly bigger than π, and fp64_sin would correctly return a very small negative number. But in both cases, fp64_sin will not return 0.

You will find the same behaviour also on other processors, computers and applications. E.g., start Excel, fill cell A1 with the formula =PI() and cell B1 with the formula =sin(A1). You will also get a value in the range of 1*10^-16 .

But why do some calculators/apps return 0? The IEEE standard does not require
transcendental functions to be exactly rounded, so there is some freedom for implementation. Also, there are different algorithms available on how to compute sin(x), like CORDIC, taylor series, or rational approximation. But all algorithms have their advantages and drawbacks.

E.g., the early version of fp64_lib used CORDIC, having the big advantage that one algorithm can be used both for calculating the trigonometric function and it’s inverse. However, CORDIC is very slow, for the required 53 bit precision over 80 iteration would be needed, and all the calculation per iteration would have to be carried out with extended precision (>53bit). I tried to sneak around with just 53 iterations with the usual 53-bit arithmetic already implemented, and beside being slow, the achieved precision was also horrible as a lot of rounding errors were accumulating up. The current fp64lib-implementation of sine and cosine uses an 8th power polynom with some tricks to achieve 52/53-bit precision across the range 0-2*π.

And based on the application, some libraries choose to round. E.g., if you have an calculator app with maximum 10 digits display, you may round the result of sin(something near to π) to 0. E.g., my HP-34C (1979-1983) returns -4.1*10^-10, whereas my Android phone standard calculator (2025, 64-bit Java double library) returns 0.

There is quite some documentation available online on the basics on how to correctly use floating point math and what to expect. Here is a short list of papers and websites, that I can recommend:

What Every Computer Scientist Should Know About Floating-Point Arithmetic, from David Goldberg, 1991, https://dl.acm.org/doi/pdf/10.1145/103162.103163 – A must-read for people with some academic/computer science background. Be prepared for some formulas, but also for a lot of insights.

What Every Programmer Should Know About Floating-Point Arithmetic, by brazzy/Michael Borgwardt, https://floating-point-gui.de/ – A small, what well made website with hands-on explanations and tipps, easy to understand.

Floating-point arithmetic – all you need to know, explained interactively, by Michael Matloka, https://matloka.com/blog/floating-point-101 – an easy to read article on how floating point arithmetic works, with a calculator that shows you live the bits of an 64-bit floating point number.

Floating Point Demystified, Part 1. by Josh Haberman, https://blog.reverberate.org/2014/09/what-every-computer-programmer-should.html – an article starting from integer math to fixed point and finally floating point math, showing also the problems when going from one data type to another.

All the documentation listed above is out there for already quite some time, but they are not at all outdated! The problems you face with floating point arithmetic are fundamentely tied to data types with a limited number of digits, being space-efficiently encoded. So, this even relevant today with new languages like Rust, or AI models running on your GPU.

And even with libraries with abritary precision, like the python Decimal library, your number of digits is limited by computer memory, and the problem of transcendential numbers will persist anyhow. So sine of any computer approximation of π will never be exactly 0 …